Last Update: February 12, 2020
Probability distributions consist of all possible values that a discrete or continuous random variable can have and their associated probability of being observed. Classical or a priori probability distribution is theoretical while empirical or a posteriori probability distribution is experimental.
This topic is part of Business Statistics with R course. Feel free to take a look at Course Curriculum.
This tutorial has an educational and informational purpose and doesn’t constitute any type of forecasting, business, trading or investment advice. All content, including code and data, is presented for personal educational use exclusively and with no guarantee of exactness of completeness. Past performance doesn’t guarantee future results. Please read full Disclaimer.
An example of probability distributions is normal probability distribution which consists of all possible values that a continuous random variable can have and their associated probability of being observed. Its probability distribution function is bell-shaped, symmetric from its mean and mesokurtic. Standard normal probability distribution consists of normal probability distribution with mean zero and unit variance. Any normal probability distribution can be converted into a standard normal probability distribution through continuous random variable standardization.
1. Formula notation.
Where = normal probability density function,
= continuous random variable,
= normal probability distribution mean,
= standard normal probability distribution mean,
= normal probability distribution variance,
= standard normal probability distribution variance,
= normal and standard normal probability distributions skewness,
= normal and standard normal probability distributions excess kurtosis,
= continuous random variable standardization,
= continuous random variable mean,
= continuous random variable standard deviation.
2. R script code example.
2.1. Load R packages [1].
library('quantmod')
library('PerformanceAnalytics')2.2. Probability distributions data reading, standardized daily returns calculation and standardized daily returns descriptive statistics output.
- Data: S&P 500® index replicating ETF (ticker symbol: SPY) daily adjusted close prices (2007-2015).
- Data daily arithmetic returns and standardized daily arithmetic returns calculation.
data <- read.csv('Probability-Distributions-Data.txt',header=T)
spy <- xts(data[,2],order.by=as.Date(data[,1]))rspy <- dailyReturn(spy)
srspy <- scale(rspy)In:
mean(srspy)
Out:
1.097695e-17In:
sd(srspy)
Out:
1In:
skewness(srspy)
Out:
0.2170076In:
kurtosis(srspy)
Out:
13.620342.3. Standardized daily returns density histogram and standard normal probability distribution curve overlay chart.
hist(srspy,freq=F)
curve(dnorm(x,mean=0,sd=1),col='blue',add=T,yaxt='n')
legend('topright',col='blue',lty=1,legend='n(m=0,sd=1)',cex=0.8)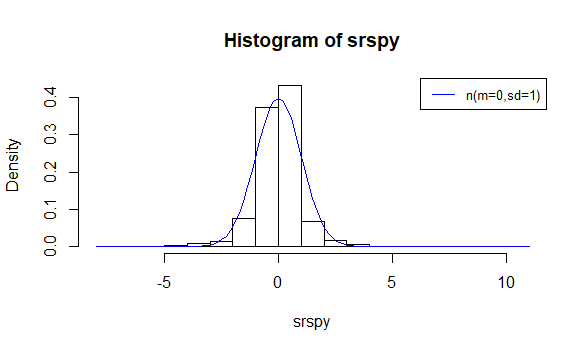
3. References.
[1] Jeffrey A. Ryan and Joshua M. Ulrich. “quantmod: Quantitative Financial Modelling Framework”. R package version 0.4-15. 2019.
Brian G. Peterson and Peter Carl. “PerformanceAnalytics: Econometric Tools for Performance and Risk Analysis”. R package version 1.5.3. 2019.