Last Update: December 15, 2020
Multiple regression assumptions consist of independent variables correct specification, independent variables no linear dependence, regression correct functional form, residuals no autocorrelation, residuals homoscedasticity and residuals normality.
This topic is part of Multiple Regression Analysis with Excel course. Feel free to take a look at Course Curriculum.
This tutorial has an educational and informational purpose and doesn’t constitute any type of business, forecasting, trading or investment advice. All content, including spreadsheet calculations and data, is presented for personal educational use exclusively and with no guarantee of exactness of completeness. Past performance doesn’t guarantee future results. Please read full Disclaimer.
Residuals homoscedasticity consists of evaluating whether regression residuals or forecasting errors have a constant variance.
This is evaluated through Breusch-Pagan heteroscedasticity test [1] which consists of using squared original regression residuals data as dependent variable together with original regression independent variables and assessing if independent variables are jointly statistically significant.
1. Formula notation.
1.1. Breusch-Pagan test formula notation.
- Note: number of original regression independent or explanatory variables not fixed and only included for educational purposes.
Where = squared original regression estimated residuals or forecasting errors,
= regression constant or intercept,
= regression coefficients,
= original regression independent or explanatory variables data,
= regression residuals or forecasting errors.
1.2. Breusch-Pagan test.
Breusch-Pagan Lagrange multiplier statistic :
- If Breusch-Pagan Lagrange multiplier statistic
level of statistical significance then residuals were heteroscedastic with
level of statistical confidence.
- If Breusch-Pagan Lagrange multiplier statistic
level of statistical significance then residuals were homoscedastic with
level of statistical confidence.
2. Excel example.
2.1. Breusch-Pagan test data.
- Data: S&P 500® index replicating ETF (ticker symbol: SPY) adjusted close prices arithmetic monthly returns, 1 Year U.S. Treasury Bill Yield, 10 Years U.S. Treasury Note Yield, Merrill Lynch U.S. High Yield Corporate Bond Index Yield effective monthly yields, U.S. Consumer Price Index, U.S. Producer Price Index monthly inflations or deflations, West Texas Intermediate Oil prices arithmetic monthly returns, U.S. Industrial Production Index value, U.S. Personal Consumption Expenditures arithmetic monthly changes (1997-2016).
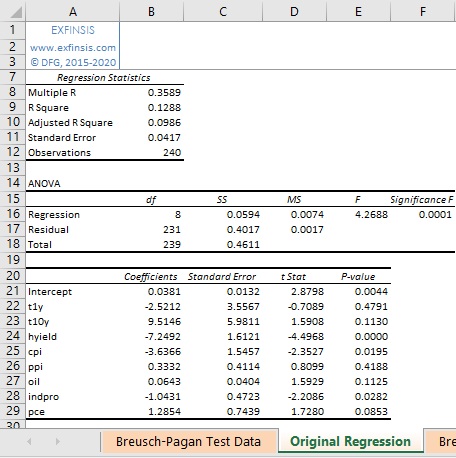
2.2. Breusch-Pagan test original multiple linear regression calculation.
- Multiple linear regression calculation done using Microsoft Excel Data Analysis® Add-In Regression Analysis Tool.
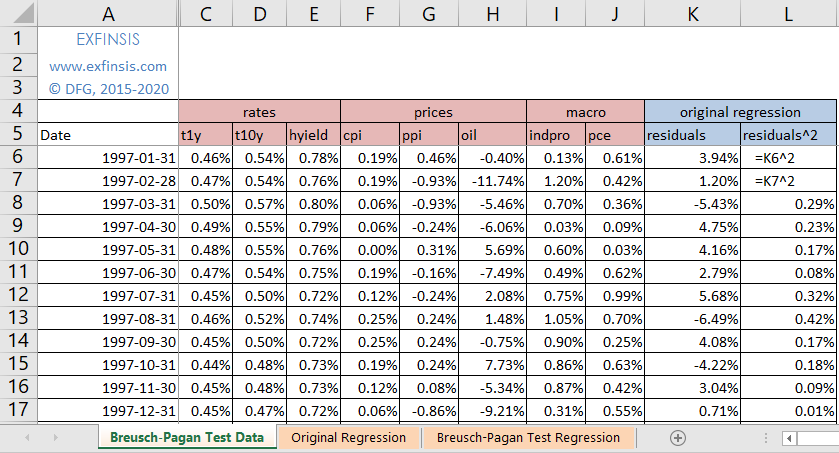
2.3. Breusch-Pagan test multiple linear regression data.
- Multiple linear regression residuals calculation done using Microsoft Excel Data Analysis® Add-In Regression Analysis Tool.
2.4. Breusch-Pagan test multiple linear regression data formulas.
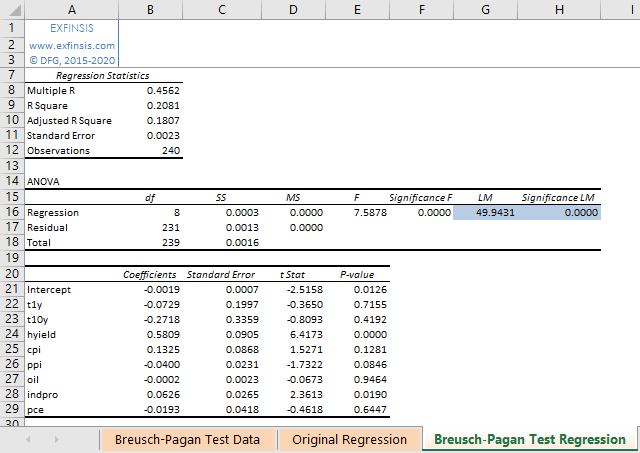
2.5. Breusch-Pagan test multiple linear regression calculation.
- Multiple linear regression calculation done using Microsoft Excel Data Analysis® Add-In Regression Analysis Tool.
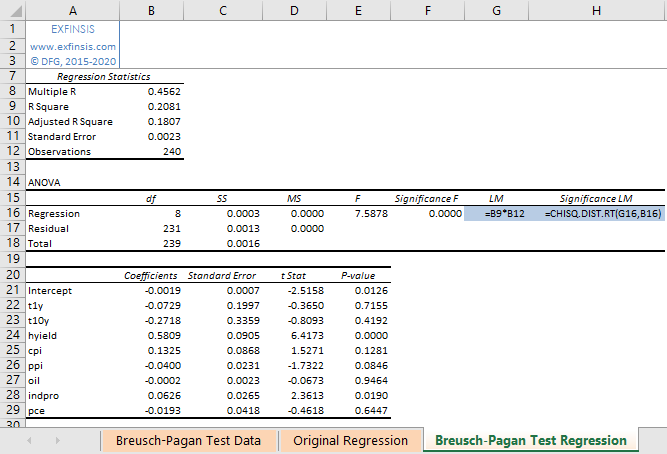
2.6. Breusch-Pagan test multiple linear regression calculation formulas.
3. References
[1] Breusch, T. S.; Pagan, A. R. “A Simple Test for Heteroskedasticity and Random Coefficient Variation”. Econometrica. 1979.