Last Update: December 15, 2020
Asset pricing models consist of estimating asset expected return through its expected risk premium linear relationship with factors portfolios expected risk premiums and macroeconomic factors.
This topic is part of Investment Portfolio Analysis with Excel course. Feel free to take a look at Course Curriculum.
This tutorial has an educational and informational purpose and doesn’t constitute any type of trading or investment advice. All content, including spreadsheet calculations and data, is presented for personal educational use exclusively and with no guarantee of exactness of completeness. Past performance doesn’t guarantee future results. Please read full Disclaimer.
An example of asset pricing models is arbitrage pricing theory APT [1] which consists of estimating asset expected return through its expected risk premium linear relationship with market portfolio expected risk premium and macroeconomic factors.
1. Formula notation.
1.1. Arbitrage pricing theory APT asset risk premium formula notation.
- Note: macroeconomic factor not fixed and only included for educational purposes.
Where = asset realized risk premiums,
= asset realized returns,
= realized risk free returns,
= asset average realized excess return,
= asset market beta coefficient,
= market realized risk premiums,
= market realized returns,
= asset macroeconomic factor beta coefficient,
= realized consumer price index percentage changes macroeconomic factor,
= linear regression residuals or forecasting errors.
1.2. Arbitrage pricing theory APT model formula notation.
- Note: APT formula recasting using expected returns (ex-ante) instead of average realized returns (ex-post). For full reference, please read The Arbitrage Theory of Capital Asset Pricing [1].
Where = asset expected return,
= expected risk-free return,
= asset market beta coefficient,
= market expected risk premium,
= market expected return,
= asset macroeconomic factor beta coefficient,
= expected percentage change in consumer price index macroeconomic factor.
2. Excel example.
2.1. APT multiple factors model data.
- Data: S&P 500® index replicating ETF (ticker symbol: SPY) adjusted close prices and market portfolio [2] monthly arithmetic returns risk premiums, U.S. consumer price index monthly arithmetic change (2007-2016).
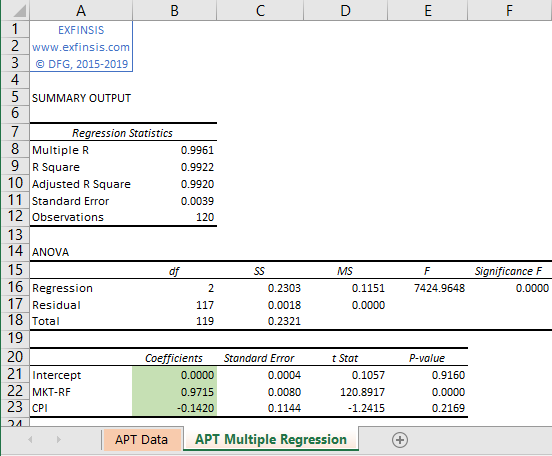
2.2. APT multiple factors model multiple linear regression calculation.
- Multiple linear regression calculation done using Microsoft Excel Data Analysis® Add-In Regression Analysis Tool.
3. References
[1] Stephen Ross. “The Arbitrage Theory of Capital Asset Pricing”. Journal of Economic Theory. 1976.
[2] Eugene F. Fama and Kenneth F. French. “Common Risk Factors in the Returns on Stocks and Bonds,” Journal of Financial Economics. 1993.